【DS】第三章-栈和队列

发表于 | 分类于
字数统计: 1.7k

第三章 栈和队列

栈

栈的特性

  栈是一种线性结构，这种特殊的线性结构有着最大的特点——后进先出(Last In First Out)。最后压入栈的元素会最先被弹出。
  由于栈只用在同一端进行插入和删除，因此我们优先选择使用顺序表，因为在顺序表的末尾插入和删除的时间复杂度都是O(1)，并且操作简单

实现

  栈的实现可以基于顺序表、链表和双端队列，这里使用最简单方法基于顺序表来实现栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <assert.h>
template<class T>
class Stack
{
public:
    //构造函数
    Stack()
        :_stack(nullptr)  
        ,_size(0)
        ,_capacity(0)
    {
    }
    //析构函数
    ~Stack()
    {
        if(_stack != nullptr)
        {
            delete[] _stack;
        }
    }
    //入栈
    void Push(const T& temp)
    {
        //尾插
        //容量检查
        if(_size == _capacity)//满了
        {
            size_t newCapacity = (_capacity == 0 ? 5 : 2 * _capacity);
            T* stackTemp = new T[newCapacity];
            for(int i = 0; i < _size; i++)
            {
                stackTemp[i] = _stack[i];
            }
            //delete空指针是完全安全的
            delete[] _stack;
            _stack = stackTemp;
            _capacity = newCapacity;
            std::cout << "Expend new capacity:" << _capacity << std::endl;
        }
        _stack[_size] = temp;
        _size++;
    }
    //出栈
    void Pop()
    {
        if(_size <= 0)
        {
            return;
        }
        _size--;
    }
    //栈顶元素
    const T& Top()
    {
        assert(_size > 0);
        return _stack[_size - 1];
    }
    //元素个数
    size_t Size()
    {
        return _size;
    }
    //是否为空
    bool IsEmpty()
    {
        return (_size <= 0 ? true : false);
    }
private:
    T* _stack;//顺序表
    size_t _size;//长度
    size_t _capacity;//容量
};

如何判断一个序列是否为出栈序列

  一个入栈序列有很多种出栈顺序，例如入栈1 2 3 4 5，他的出栈序列可以是5 4 3 2 1也可也是3 2 1 4 5，那么如何判断一个序列是否是一个入栈序列的出栈序列呢？
  这道题的思路很简单，我们需要利用一个栈和两个分别指向入栈序列和出栈序列的指针。当栈为空或栈顶元素不等于当前出栈序列指针所指元素时，将入栈序列指针所指元素压入栈，并且入栈序列指针后移；如果相同则将栈顶元素弹出并将出栈序列指针后移。如果在演算过程中还需要向栈中压入元素而入栈序列已经被全部遍历指针指向队尾则可以怕判断当前序列不是入栈序列的出栈序列；如果可以同时遍历完入栈序列和出栈序列并且栈为空则当前序列时一个入栈序列的出栈序列。

https://misakifx.github.io/2019/10/25/%E3%80%90DS%E3%80%91%E6%A0%88%E7%9A%84%E5%8E%8B%E5%85%A5%E3%80%81%E5%BC%B9%E5%87%BA%E5%BA%8F%E5%88%97/

  

栈的应用

  栈有以下几种应用：判断括号匹配，后缀表达式，迷宫的暴力破解法等。

队列

队列的特点

  队列也是一种线性结构，这种线性结构的特点为先进先出(First in First out)。由于队列需要在队列两端进行插入或删除，因此我们优先选择链表来进行实现。当然使用数组实现也可以，只是数组在头部插入和删除元素需要ON的时间复杂度，因此选择链表更优。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include <iostream>
#include <assert.h>
template<class T>
struct QueueNode
{
    QueueNode()
        :_data(T())
        ,_next(nullptr)
    {}
    QueueNode(const T& data, QueueNode* next)
        :_data(data)
        ,_next(next)
    {}
    T _data;
    QueueNode* _next;
};

//用单向带头不循环链表实现队列
template<class T>
class Queue
{
public:
    Queue()
        :_head(nullptr)
        ,_rear(nullptr)
        ,_size(0)
    {
        _head = new QueueNode<T>;
        _rear = _head;
    }
    ~Queue()
    {
        while(!Empty())
        {
            Pop();
        }
        delete _head;
        _head = nullptr;
        _rear = nullptr;
    }
    void Push(const T& data)
    {
        QueueNode<T>* newNode = new QueueNode<T>(data, nullptr);
        _rear->_next = newNode;
        _rear = newNode;
        _size++;
    }
    bool Empty()
    {
        return _rear == _head;
    }
    void Pop()
    {
        QueueNode<T>* temp = _head->_next;
        _head->_next = _head->_next->_next;
        //队列中只有一个元素
        if(temp == _rear)
        {
            _rear = _head;
        }
        delete temp;
        temp = nullptr;
        _size--;
    }
    const T& Front()
    {
        assert(_head->_next != nullptr);
        return _head->_next->_data;
    }
    const T& Back()
    {
        assert(_rear != _head);
        return _rear->_data;
    }
    size_t Size()
    {
        return _size;
    }
private:
    QueueNode<T>* _head;    //指向头部结点
    QueueNode<T>* _rear;    //指向最后一个元素
    size_t _size;
};

int main()
{
    Queue<int> que;
    que.Push(1);
    que.Push(2);
    que.Push(3);
    que.Push(4);
    while(!que.Empty())
    {
        std::cout << "size = " << que.Size() << std::endl;
        std::cout << que.Front() << std::endl;
        que.Pop();
    }
}



size = 4
1
size = 3
2
size = 2
3
size = 1
4

  以上代码完成了队列的基本功能。

环形队列

环形队列实现思路

  环形队列是一种特殊的队列，队列依然保证先进先出的特点，但是在逻辑结构上队列呈一个环状，可以保证在给定的有限空间内利用数组实现操作达到O1的队列。其需要用到两个指针，一个指针head指向向队头，一个指针rear指向队尾的后一个位置用来标记当前队列空间的使用情况，如果队满则禁止继续插入。
  当插入元素时，将元素插入到队尾指针指向的位置，然后将rear指针后移；当弹出元素时只需将head指针后移即可。但是要注意由于是环形队列，因此当两个指针走到数组末尾时需要做特殊处理让他们重新指回到数组头部。
  但是环形队列两个指针的位置都是不固定的，我们又该如何判断队满和队空以及计算数组元素呢？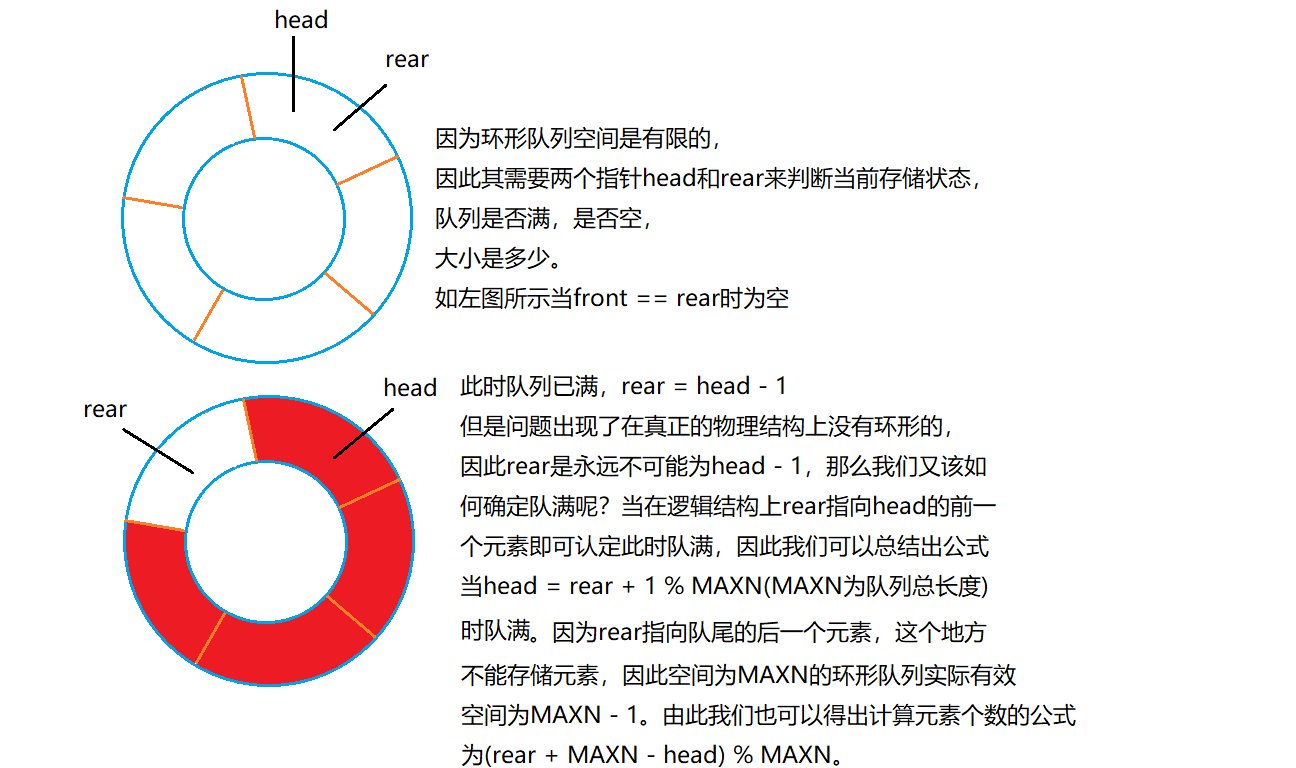

环形队列

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <iostream>
#include <assert.h>

template<class T>
class CircleQueue
{
public:
    CircleQueue(size_t capacity)
        :_arr(nullptr)
        ,_head(0)
        ,_rear(0)
        ,_capacity(capacity)
    {
        assert(capacity >= 2);
        _arr = new T[_capacity];
    }
    ~CircleQueue()
    {
        delete _arr;
        _arr = nullptr;
    }
    //判断满
    bool IsFull()
    {
        if((_rear + 1) % _capacity == _head)
        {
            return true;
        }
        return false;
    }
    ///判断空
    bool IsEmpty()
    {
        if(_head == _rear)
        {
            return true;
        }
        return false;
    }
    bool Push(const T& data)
    {
        if(IsFull())
        {
            return false;
        }
        _arr[_rear] = data;
        _rear = (_rear + 1) % _capacity; 
        return true;
    }
    bool Pop()
    {
        if(IsEmpty())
        {
            return false;
        }
        _head = (_head + 1) % _capacity;
        return true;
    }
    const T& Front()
    {
        assert(!IsEmpty());
        return _arr[_head];
    }
    const T& Back()
    {
        assert(!IsEmpty());
        size_t temp = (_rear + _capacity - 1) % _capacity;
        return _arr[temp];
    }
    size_t Capacity()
    {
        return _capacity;
    }
    size_t Size()
    {
        return (_rear + _capacity - _head) % _capacity;
    }
private:
    T* _arr;            //存储环形队列的数组
    size_t _head;       //指向队头
    size_t _rear;       //指向队尾
    size_t _capacity;   //环形队列的总容量，一旦确定不可再改变
};

int main()
{
    CircleQueue<int> circleQueue(5);
    circleQueue.Push(1);
    circleQueue.Push(2);
    circleQueue.Push(3);
    circleQueue.Push(4);
    circleQueue.Push(5);
    while(!circleQueue.IsEmpty())
    {
        std::cout << "size = " << circleQueue.Size() << std::endl;
        std::cout << circleQueue.Front() << std::endl;
        circleQueue.Pop();
    }
    //std::cout << circleQueue.Front() << std::endl;
}


size = 4
1
size = 3
2
size = 2
3
size = 1
4

  以上实现了环形队列的基本功能。

-------------本文结束感谢您的阅读!-------------
记录学习每一分，感谢您的赞助