排序
基本概念
本章会介绍并且实现,常用的几种排序算法及其思想,但是关于排序除了时间复杂度和空间复杂度这两个衡量算法的基本标准外,还引入了稳定的概念。
稳定
如果一个排序算法排序结束后,表中相同大小的元素依然可用保持和排序前一样的相对顺序则称该排序是稳定的,反之是不稳定的。
举个例子,以下这个序列中,出现了相同的元素3,为了便于区分,我将其中一个用红色标记出来。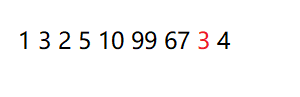
如果我们进行了某种排序算法将其进行了排序,并且排序结果如下。
我们发现结果中红色的3与黑色的3相比排序前的序列依然保持着黑色在前红色在后的相对顺序,此时我们则称这个排序是稳定的,但是如果排序后有可能会使任意一组相同元素的相对顺序出现了改变,则称其是不稳定的。
注意稳定度是一个排序的基本性质,一次结果是稳定的不能说排序是稳定的,必须保证每次都是稳定的才可以说这个排序是稳定的,这就需要根据排序的思想来判断其是否稳定。
冒泡排序
冒泡排序属于交换排序的一种,以升序排序为例,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。这样的过程十分类似于水泡上浮冒泡的过程,所以成为冒泡排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36#include <iostream>
#include <vector>
void BubbleSort(std::vector<int>& arr)
{
int n = arr.size();
bool flag = true;
for(int i = 0; i < n - 1; i++)
{
if(flag == false)
{
break;
}
flag = false;
for(int j = 0; j < n - i - 1; j++)
{
if(arr[j] > arr[j + 1])
{
flag = true;
std::swap(arr[j], arr[j + 1]);
}
}
}
}
int main()
{
std::vector<int> arr = {1, 1, 2, 2, 99, 3, 3, 4, 5, 88, 2};
BubbleSort(arr);
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 1 2 2 2 3 3 4 5 88 99
冒泡排序十分容易理解,但它是一种十分低效的算法,其时间复杂度为ON^2,空间复杂度为O1,但是该算法是稳定的。
直接插入排序
直接插入排序属于插入排序的一种,插入排序是将序列分为两部分,一部分为已经有序部分,一部分为未有序部分。遍历未有序部分将该部分第一个元素插入到有序序列中的合适位置,遍历完毕则完成了排序。
但是在实际实现时为了简化操作,具体流程为将未有序部分与有序部分最后一个比较,如果不满足排序要求则交换,继续与倒数第二个元素比较以此类推,直到满足排序顺序为止。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32#include <iostream>
#include <vector>
void InsertSort(std::vector<int>& arr)
{
if(arr.size() <= 1)
{
return;
}
int n = arr.size();
for(int i = 1; i < n; i++)
{
int j = i - 1;
while(arr[j] > arr[j + 1] && j >= 0)
{
std::swap(arr[j], arr[j + 1]);
j--;
}
}
}
int main()
{
std::vector<int> arr = {1, 1, 99, 23, 32, 2, 2, 4, 5};
InsertSort(arr);
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 1 2 2 4 5 23 32 99
直接插入排序也是十分容易理解的排序,但是同样的效率十分低下,其时间复杂度为ON^2,空间复杂度为O1,但是它同样是稳定的。
选择排序
选择排序同样是将序列分为两个部分,一个部分为有序部分,一个为无序部分,以升序为例,选择排序每次都从无序部分中选一个最小的放到有序序列的末尾,当无序部分全部变为有序部分则排序结束。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34#include <iostream>
#include <vector>
void SelectSort(std::vector<int>& arr)
{
int n = arr.size();
for(int i = 0; i < n - 1; i++)
{
int min = i;
for(int j = i + 1; j < n; j++)
{
if(arr[j] < arr[min])
{
min = j;
}
}
if(min != i)
{
std::swap(arr[i], arr[min]);
}
}
}
int main()
{
std::vector<int> arr = {1, 2, 3, 19, 10, 5, 2, 5, 7};
SelectSort(arr);
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 2 2 3 5 5 7 10 19
选择排序也是十分容易理解但是效率较低的排序方式,其时间复杂度为ON^2,空间复杂度为O1,但是它也是稳定的。
希尔排序
希尔排序是插入排序的升级版本。因为插入排序对于越有序的序列所用排序时间越短,时间复杂度越低的特性,希尔排序旨在使用插入排序使每次排序的序列要么足够短,要么就几乎已经有序,来极大程度节省时间,提高效率。
希尔排序思想是将序列通过间隔分为若干子序列,对这些子序列先进行排序,每次减小间隔直到1,就完全变成了直接插入排序,不过此时序列已经几乎有序,可用大大提高直接插入排序的效率。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40#include <iostream>
#include <vector>
void InsertSort(int gap, std::vector<int>& arr)
{
int n = arr.size();
for(int i = gap; i < n; i++)
{
for(int j = i - gap; j >= 0; j -= gap)
{
if(arr[j + gap] >= arr[j])
{
break;
}
else
{
std::swap(arr[j + gap], arr[j]);
}
}
}
}
void ShellSort(std::vector<int>& arr)
{
for(int i = arr.size() / 2; i >= 1; i /= 2)
{
InsertSort(i, arr);
}
}
int main()
{
std::vector<int> arr = {1, 2, 10, 3, 4, 7, 2, 9, 3, 4, 99, 5};
ShellSort(arr);
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 2 2 3 3 4 4 5 7 9 10 99
希尔排序是直接插入排序的升级版本,因此它利用自己本身的特性提高了插入排序的效率,平均情况下,它的时间复杂度可用达到ONlogN~ON^2,空间复杂度为O1,但是希尔排序是不稳定的。
堆排序
堆排序时利用二叉树的顺序结构建成二叉堆,利用堆进行排序的排序算法,算法分为两个部分。
首先要对序列建堆,建堆思路及从最后一个父结点开始向下调整,直到第一个父结点为止。
建好堆后将堆顶元素弹出,即将堆顶元素与最后一个元素交换,然后弹出最后一个元素,然后对堆顶进行一次向下调整,此为一次排序,不断重复进行排序,直到堆为空为止,则排序完成。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56#include <iostream>
#include <vector>
//堆排序最简单的实现方法就是使用STL中的优先级队列
//优先级队列内部自动维护了一个堆,可用很轻松的帮助我们完成堆排序
//但是为了更好的了解算法思想这里我们手动维护这个堆
void AdjustDown(int start, int end, std::vector<int>& arr)
{
int parent = start;
int child = parent * 2 + 1;
while(child < end)
{
if(child + 1 < end && arr[child + 1] > arr[child])
{
child += 1;
}
if(arr[child] <= arr[parent])
{
break;
}
else
{
std::swap(arr[child], arr[parent]);
parent = child;
child = parent * 2 + 1;
}
}
}
void HeapSort(std::vector<int>& arr)
{
//建堆
int n = arr.size();
for(int i = (n / 2 - 1); i >= 0; i--)
{
AdjustDown(i, n, arr);
}
//排序
while(n > 0)
{
std::swap(arr[0], arr[n - 1]);
n--;
AdjustDown(0, n, arr);
}
}
int main()
{
std::vector<int> arr = {1, 4, 5, 3, 4, 22, 33, 5, 2};
HeapSort(arr);
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 2 3 4 4 5 5 22 33
堆排序的效率较高,并且序列越无序则效率越高,它的时间复杂度为ONlogN,空间复杂度为O1,但它是不稳定的。
归并排序
归并排序的思想是将序列首先拆分成若干不可再分的子序列,然后再将它们一一合并达到有序的效果。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66#include <iostream>
#include <vector>
//左闭右开区间
void Merge(std::vector<int>& arr, int start, int mid, int end)
{
std::vector<int> arr1, arr2;
for(int i = start; i < mid; i++)
{
arr1.push_back(arr[i]);
}
for(int i = mid; i < end; i++)
{
arr2.push_back(arr[i]);
}
int i = 0, j = 0, k = start;
while(i < arr1.size() && j < arr2.size())
{
if(arr1[i] <= arr2[j])
{
arr[k] = arr1[i];
i++;
k++;
}
else
{
arr[k] = arr2[j];
j++;
k++;
}
}
while(i < arr1.size())
{
arr[k] = arr1[i];
i++;
k++;
}
while(j < arr2.size())
{
arr[k] = arr2[j];
j++;
k++;
}
}
void MergeSort(std::vector<int>& arr, int start, int end)
{
if(end - start > 1)
{
int mid = (start + end) >> 1;
MergeSort(arr, start, mid);
MergeSort(arr, mid, end);
Merge(arr, start, mid, end);
}
}
int main()
{
std::vector<int> arr = {1, 2, 22, 1, 5, 4, 55, 44, 3};
MergeSort(arr, 0, arr.size());
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 1 2 3 4 5 22 44 55
对其进行改进可以写成以下的样子。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66#include <iostream>
#include <vector>
//左闭右开区间
void Merge(std::vector<int>& arr, int start, int mid, int end)
{
std::vector<int> arr1, arr2;
for(int i = start; i < mid; i++)
{
arr1.push_back(arr[i]);
}
//for(int i = mid; i < end; i++)
//{
// arr2.push_back(arr[i]);
//}
int i = 0, j = mid, k = start;
while(i < arr1.size() && j < end)
{
if(arr1[i] <= arr[j])
{
arr[k] = arr1[i];
i++;
k++;
}
else
{
arr[k] = arr[j];
j++;
k++;
}
}
while(i < arr1.size())
{
arr[k] = arr1[i];
i++;
k++;
}
//while(j < arr2.size())
//{
// arr[k] = arr2[j];
// j++;
// k++;
//}
}
void MergeSort(std::vector<int>& arr, int start, int end)
{
if(end - start > 1)
{
int mid = (start + end) >> 1;
MergeSort(arr, start, mid);
MergeSort(arr, mid, end);
Merge(arr, start, mid, end);
}
}
int main()
{
std::vector<int> arr = {1, 2, 22, 1, 5, 4, 55, 44, 3};
MergeSort(arr, 0, arr.size());
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 1 2 3 4 5 22 44 55
归并排序相比内排序更广泛适用于外排序中,在需要有大量数据进行排序的时候需要使用外排序局部读入内存再进行合并的方式进行排序。它的时间复杂度为ONlogN,空间复杂度为ON,并且它是稳定的。
快速排序
快速排序是基本排序算法中最快的排序,他和归并算法一样用了分治的思想。它的思路是每次将序列的第一个元素排到合适的位置,使该元素前面的元素都不大于它,后面的元素都不小于它,然后递归整理前面的元素和后面的元素,使所有元素前面的元素都不大于它,后面的元素都不小于它即完成有序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51#include <iostream>
#include <vector>
//左闭右开区间
void QuickSort(std::vector<int>& arr, int start, int end)
{
if(end - start <= 1)
{
return;
}
int temp = arr[start];
int ptr1 = start;
int ptr2 = end - 1;
while(ptr1 < ptr2)
{
while(arr[ptr2] >= temp && ptr1 < ptr2)
{
ptr2--;
}
if(ptr1 >= ptr2)
{
break;
}
arr[ptr1] = arr[ptr2];
while(arr[ptr1] <= temp && ptr1 < ptr2)
{
ptr1++;
}
if(ptr1 >= ptr2)
{
break;
}
arr[ptr2] = arr[ptr1];
}
arr[ptr1] = temp;
QuickSort(arr, start, ptr1);
QuickSort(arr, ptr1 + 1, end);
}
int main()
{
std::vector<int> arr = {3, 1, 2, 55, 2, 4, 88, 22, 1, 3};
QuickSort(arr, 0, arr.size());
for(const auto& e : arr)
{
std::cout << e << " ";
}
}
1 1 2 2 3 3 4 22 55 88
快排使最快的基本排序算法,并且同样的是越有序则排序越快。它的时间复杂度为ONlogN,空间复杂度为OlogN~ON,但它是不稳定的。

