树的概念及结构
什么是树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:每个结点有零个或多 个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结 点可以分为多个不相交的子树。
下图就是一棵常见的树。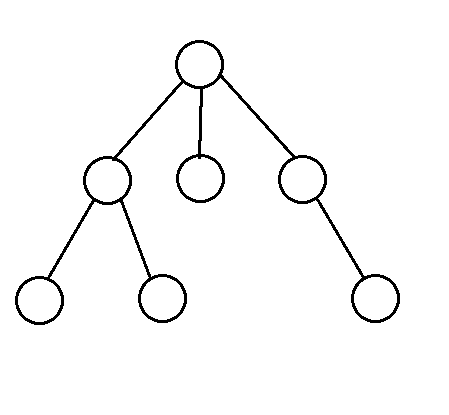
树的常用名词
节点的度:一个节点含有的子树的个数称为该节点的度;
叶节点或终端节点:度为0的节点称为叶节点;
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的度:一棵树中,最大的节点的度称为树的度;
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推; 树的高度或深度:树中节点的最大层次; 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙; 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的表示
树的表示相比线性结构就要复杂一些,因为其是层次结构的,其的下一个结点可能有多个,也可能只有一个,因此十分难以在逻辑结构上进行表示。于是伟大的人类提出了一种方法可以很简单的表示任意一棵二叉树,这种表示方法称之为孩子兄弟表示法。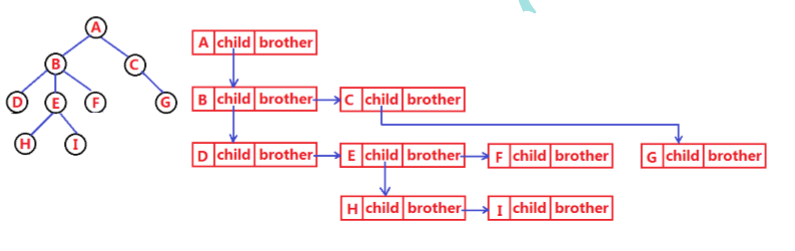
所谓孩子兄弟表示法就是让任何一个结点仅指向它的第一个孩子结点和右边相邻的兄弟结点(如果没有孩子或兄弟指向空),由此任意一棵树上的任何一个节点都可以变成一个度最大仅为2结点,由此我们可以将任何一棵树都变成一棵二叉树。
二叉树
什么是二叉树
二叉树是一棵所有节点的度最大为2的树。任何一棵树都可以通过孩子兄弟表示法转换为二叉树,因此我们接下来的所有研究都是围绕二叉树进行的。下图就是一棵二叉树。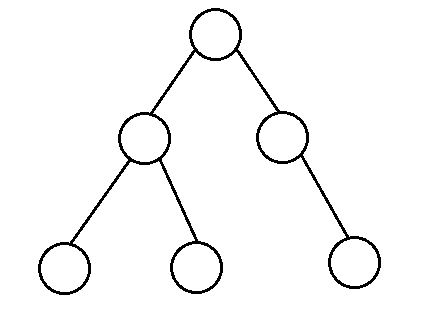
二叉树的特点
1. 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,其子树的次序不能颠倒。
3.若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0)。
4.高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)。 (空树的高度为-1)
5.对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
特殊的二叉树
完美二叉树(满二叉树)
一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树。意思是说这棵深度为k的二叉树任意一行的结点都已经是满的了。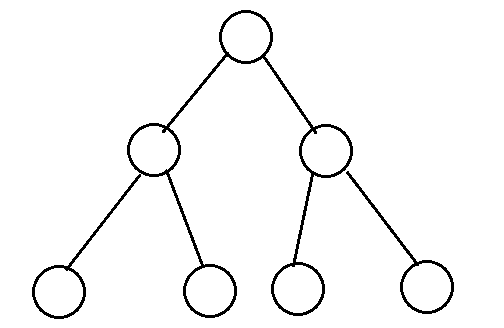
完全二叉树
完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。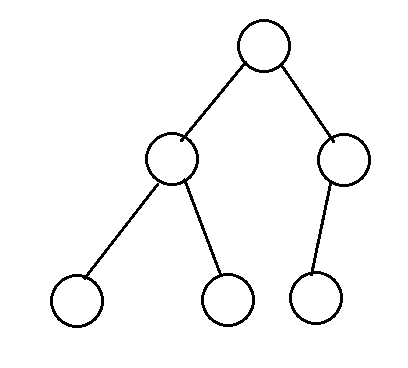
完满二叉树
所有非叶子结点的度都是2
换句话说就是只要你有孩子,你就必然是有两个孩子。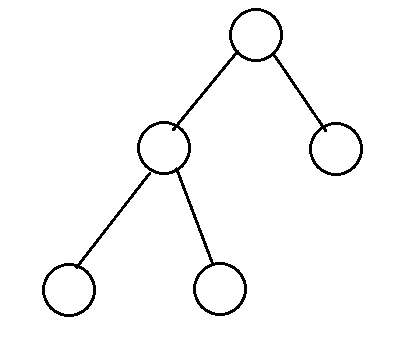
二叉树的存储
顺序存储
顺序存储指的是利用链表在连续的地址空间上进行存储。但是顺序存储只适用于完全二叉树,因为这样才不会有空间的浪费,所以顺序的存储方式一般用来存储堆。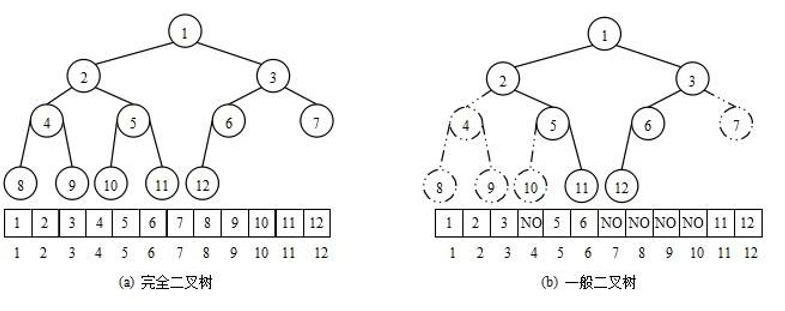
链式存储
链式的二叉树存储方式是最为常用的二叉树存储形式,用一个二叉链(或三叉链)的形式来构成二叉树。
二叉链
如下是一个二叉链的存储形式。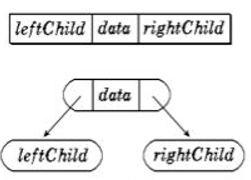
二叉链结构:1
2
3
4
5
6struct BinaryTreeNode
{
T _data;
BinaryTreeNode<T>* _left;
BinartTreeNode<T>* _right;
};
三叉链
如下是一个三叉链的存储形式。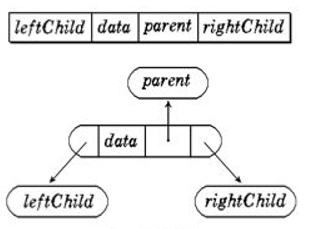
二叉链解雇:1
2
3
4
5
6
7
8template<class T>
struct BinaryTreeNode
{
T _data;
BinaryTreeNode<T>* _left;
BinartTreeNode<T>* _right;
BinartTreeNode<T>* _parent;//多了一个指向父亲的指针
};
堆
堆的概念
堆是典型的通过使用顺序方式存储二叉树来实现的数据结构,因为堆可以保证其必然是一棵完全二叉树。
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆有两点性质:
1、其保证其一定是一棵完全二叉树。
2、堆中任意一个孩子结点必不大于(大根堆)或者不小于(小根堆)其父结点。
下图是一个小根堆: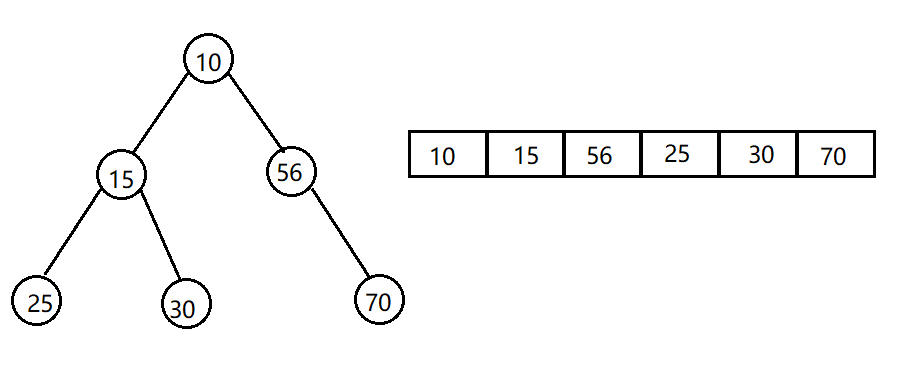
下图是一个大根堆: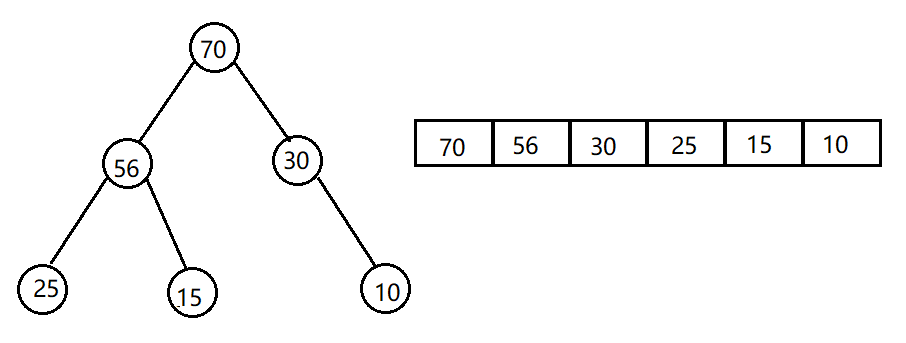
堆的实现
堆的实现中有三个基础操作,向上调整,向下调整以及建堆,他们三个共同构成了堆的所有基础操作。STL中的优先级队列底层就是一个堆,所以平时要使用堆的时候我们不必自己写一个,可以借助优先级队列来实现。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159#include <iostream>
#include <vector>
#include <algorithm>
#include <assert.h>
//T为数据类型,Compare为比较方法,less创建大根堆,greater创建大根堆
template<class T, class Compare>
class Heap
{
public:
Heap()
:_arr()
,_size(0)
{}
Heap(const std::vector<T>& arr)
:_arr(arr)
,_size(arr.size())
{
//根据已有数组建堆
//建堆思路即从最后一个开始进行向下调整,一直向下调整到根
for(int i = (_size - 2) / 2; i >= 0; i--)
{
AdjustDown(i);
}
}
void Pop()
{
//弹出根节点
//思路是将根与最后一个元素交换,然后向下调整,之后弹出最后一个结点
std::swap(_arr[0], _arr[_size - 1]);
_arr.pop_back();
_size--;
AdjustDown(0);
}
void Push(const T& data)
{
_arr.push_back(data);
//新插入元素要向上调整保证依然是一个堆
_size++;
AdjustUp(_size - 1);
}
void Print()
{
for(const auto& e : _arr)
{
std::cout << e << " ";
}
std::cout << std::endl;
}
const T& Top()
{
assert(_size > 0);
return _arr[0];
}
bool Empty()
{
assert(_size > 0);
return _size == 0;
}
size_t Size()
{
return _size;
}
void HeapSort(std::vector<int>& arr)
{
//堆排序的思想即建堆将根持续弹出放到尾部
//升序建大根堆
//降序建小根堆
Heap<T, Compare> tempHeap(_arr);
int tempSize = tempHeap.Size();
arr.resize(tempSize);
while(!tempHeap.Empty())
{
T top = tempHeap.Top();
arr[tempSize - 1] = top;
tempSize--;
tempHeap.Pop();
}
}
private:
//向下调整
//向下调整是堆操作中十分常用的基础操作
//即我们从一个指定结点开始向下调整直到不需要调整为止,
//保证调整过的路径满足堆的要求
void AdjustDown(size_t pos)
{
Compare cmp;
//孩子节点下标为 根节点下标 * 2 + 1 和 根结点下标 * 2 + 2
size_t child = pos * 2 + 1;
while(child < _size)
{
if((child + 1) < _size && cmp(_arr[child], _arr[child + 1]))
{
child += 1;
}
//如果调整了还需要继续向下调整
if(cmp(_arr[pos], _arr[child]))
{
std::swap(_arr[pos], _arr[child]);
}
else
{
break;
}
pos = child;
child = pos * 2 + 1;
}
}
//向上调整与向下调整类似
void AdjustUp(size_t pos)
{
Compare cmp;
//父结点下标为 (孩子结点下表 - 1) / 2
size_t parent = (pos - 1) / 2;
while(pos > 0)
{
//如果调整了需要继续向上迭代调整
if(cmp(_arr[parent], _arr[pos]))
{
std::swap(_arr[parent], _arr[pos]);
}
else
{
break;
}
pos = parent;
parent = (pos - 1) / 2;
}
}
private:
std::vector<T> _arr;
size_t _size;
};
int main()
{
std::vector<int> arr = {1, 2, 3, 4, 5, 6, 7};
Heap<int, std::less<int>> heap(arr);
heap.Print();
heap.Pop();
heap.Print();
std::vector<int> arr2;
heap.HeapSort(arr2);
for(const auto& e : arr2)
{
std::cout << e << " ";
}
std::cout << std::endl;
std::cout << heap.Size() << std::endl;
heap.Push(7);
heap.Print();
}
7 5 6 4 2 1 3
6 5 3 4 2 1
1 2 3 4 5 6
6
7 5 6 4 2 1 3
二叉链实现二叉树
二叉树的顺序存储代表为堆,那么链式存储典型就是使用二叉链实现二叉树。
二叉链没什么基础知识了,这里要重点关注的是我们如何在二叉链存储结构下前序,中序,后序以及层序遍历二叉树,这里简单的方法要用到递归。
实现
直接上代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167#include <iostream>
#include <queue>
//二叉链结构
template<class T>
struct BinaryTreeNode
{
BinaryTreeNode(const T& data = T())
:_data(data)
,_left(nullptr)
,_right(nullptr)
{}
T _data;
BinaryTreeNode<T>* _left;
BinaryTreeNode<T>* _right;
};
template<class T>
class BinaryTree
{
public:
BinaryTree()
:_head(nullptr)
,_size(0)
{}
BinaryTree(const std::string& preOrder)
{
int i = 0;
_head = CreateByPreOrder(preOrder, i);
}
//前序遍历
void PreOrder()
{
PreOrderCore(_head);
}
//中序遍历
void InOrder()
{
InOrderCore(_head);
}
//后序遍历
void PostOrder()
{
PostOrderCore(_head);
}
//层序遍历
void LevelOrder()
{
std::queue<BinaryTreeNode<T>*> que;
que.push(_head);
while(!que.empty())
{
BinaryTreeNode<T>*temp = que.front();
que.pop();
if(temp == nullptr)
{
std::cout << "#";
}
else
{
std::cout << (char)(temp->_data + 'A');
que.push(temp->_left);
que.push(temp->_right);
}
}
}
//判断是不是一棵完全二叉树
//层序遍历二叉树,遍历到第一个nullptr结点,
//就遍历整个队列,如果全为空则是完全二叉树
//否则就不是
bool IsComplateTree()
{
std::queue<BinaryTreeNode<T>*> que;
que.push(_head);
while(!que.empty())
{
BinaryTreeNode<T>* temp = que.front();
que.pop();
if(temp == nullptr)
{
break;
}
else
{
que.push(temp->_left);
que.push(temp->_right);
}
}
while(!que.empty())
{
BinaryTreeNode<T>* temp = que.front();
que.pop();
if(temp != nullptr)
{
return false;
}
}
return true;
}
private:
void InOrderCore(BinaryTreeNode<T>* root)
{
if(root == nullptr)
{
std::cout << "#";
return;
}
InOrderCore(root->_left);
std::cout << (char)(root->_data + 'A');
InOrderCore(root->_right);
}
void PreOrderCore(BinaryTreeNode<T>* root)
{
if(root == nullptr)
{
std::cout << "#";
return;
}
std::cout << (char)('A' + root->_data);
PreOrderCore(root->_left);
PreOrderCore(root->_right);
}
void PostOrderCore(BinaryTreeNode<T>* root)
{
if(root == nullptr)
{
std::cout << "#";
return;
}
PostOrderCore(root->_left);
PostOrderCore(root->_right);
std::cout << (char)('A' + root->_data);
}
BinaryTreeNode<T>* CreateByPreOrder(const std::string& preOrder, int& i)
{
if(preOrder[i] != '#')
{
BinaryTreeNode<T>* root = new BinaryTreeNode<T>(preOrder[i] - 'A');
root->_left = CreateByPreOrder(preOrder, ++i);
root->_right = CreateByPreOrder(preOrder, ++i);
return root;
}
else
{
return nullptr;
}
}
private:
BinaryTreeNode<T>* _head; //与链表一样存储一个头结点即可
size_t _size; //节点个数
};
int main()
{
BinaryTree<int> tree("ABD##E##CF##G##");
tree.PreOrder();
std::cout << std::endl;
tree.InOrder();
std::cout << std::endl;
tree.PostOrder();
std::cout << std::endl;
tree.LevelOrder();
std::cout << std::endl;
std::cout << "Is Complate Tree: " << tree.IsComplateTree() << std::endl;;
}

