【Cpp】第十七章-unordered版本关联式容器

发表于 | 分类于
字数统计: 6.5k

unordered系列关联式容器

什么是unordered系列

  unordered系列的关联式容器有unordered-map/unordered-set/unordered-multimap/unordered-multiset，这些版本的关联式容器和普通版本的又有什么区别呢？我们简单使用下和普通版本的做一个对比。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <map>
#include <unordered_map>
int main()
{
    std::map<int, int> m;
    m.insert(std::make_pair(1, 1));
    m.insert(std::make_pair(4, 4));
    m.insert(std::make_pair(2, 2));
    m.insert(std::make_pair(4, 4));
    m.insert(std::make_pair(6, 6));
    std::cout << "map:" << std::endl;
    for(auto e : m)
    {
        std::cout << e.first << " " << e.second << std::endl;
    }
    std::unordered_map<int, int> um;
    um.insert(std::make_pair(1, 1));
    um.insert(std::make_pair(4, 4));
    um.insert(std::make_pair(2, 2));
    um.insert(std::make_pair(4, 4));
    um.insert(std::make_pair(6, 6));
    std::cout << "unordered-map:" << std::endl;
    for(auto e : um)
    {
        std::cout << e.first << " " << e.second << std::endl;
    }

}


map:
1 1
2 2
4 4
6 6
unordered-map:
6 6
2 2
1 1
4 4

  对比结果很明显，我们发现map往往会将插入的键值对按照key的大小比较排序，因此打印出来的数据是有序的，因为其底层是一棵红黑树，因此这样的结果也是理所应当的，但是unordered-map就如它的名字一样遍历出来的数据是无序的，但是依然能完成键值对的查找功能，unordered-map与map最为显著的差距就在这里，看上去unordered-map并不如map强大，那为什么还要存在unordered系列呢？因为其查找索引能够达到O1的时间复杂度，比红黑树更快，因为其底层数据结构是一个哈希桶，关于底层实现我们之后再讨论，我们解析来首先介绍一下unordered系列的使用。

unordered系列的使用

  unordered系列共有四种关联式容器，与普通版本的互相对应，除了数据在内部存储及遍历结果无序外，其他的使用方法与普通版本的几乎没有区别，因此这里不再详细讨论接口的使用，我们这里主要要关心的是为什么unordered系列可以在舍弃有序的情况下变得更快，其底层的数据结构又是怎么样的。

底层结构

  虽然看上去unordered系列关联式容器的使用方法与普通版本的关联式容器使用没有太大区别，但他们两个的底层实现却完全不一样，这也是导致为什么unordered可以更快，并且不能有序的原因。

哈希表

什么是哈希表

  哈希表是一种根据映射来存储数据的结构，我们可以自定义一个哈希函数，通过key和哈希函数算出各个value实际在空间中存储的位置，然后进行value的存储，我们想要查找某个数据的时候也只需要通过同样的方法找到对应位置就可以拿到value。
  举个例子，我们现在有个数组，我们约定数组对应下标就存储对应key的数据value。如arr[1] = value1, arr[2] = value2, ... , arr[n] = valuen。由此一来我们想要根据key查找某个value就直接访问数组中对应下标的元素arr[key]即可。例如我们要找key == 1时value的值，我们直接访问arr[1]就可以直接拿到value1，这就是通过哈希建立映射的方法，并且这里的查找速度只需要O1，这就是典型的以空间换时间的做法，因为这里可能会出现空间的大量浪费。如果发生这么一种情况，key的上限过大，几千万或者几亿，但是中间的数据可能十分零散，此时我们为了继续建立映射不得不创建一个长度为几千万甚至几忆的数组，并且由于数据十分零散，会导致中间可能会有很多空间根本没有映射来存value，例如现在要存储两个映射key == 1, key == 10000000，我们发现这两个映射之间在没有其他映射了，那么这一个长度为10000000的数组中就只存了两个值，由此就算我们节省了时间却浪费了过多的空间，这也是哈希所要解决的一个问题。总之哈希表就是这么一种通过哈希函数建立key和value之间映射的结构。

哈希函数

  正如刚才所说，我们的value得通过哈希函数和key来确定数据存放位置并且也能找到对应数据，因此哈希函数的确定十分重要，向我们刚刚所举的例子中我们采用的哈希函数就是直接导致我们造成大量空间浪费的原因，因此在适当的时机选取何时的哈希函数也是十分重要的，接下来简单介绍几种哈希函数。

直接定址法

  取关键字的某个线性函数为散列地址：Hash(key) = A * key + b。这种哈希函数的优点也很明显，十分简单，均匀，但是它只适用于key的范围确定，且值较小还比较连续的情景，一但key过大，或者不连续就会出现大量空间被浪费的情况。

除留余数法

  这种方法是最为常用的哈希函数。假设我们散列表中允许的最大地址为m，我们可以取一个小于等于m的质数p作为除数，然后执行哈希函数Hash(key) = key % p(p <= m)，将余数作为地址进行定址。一般来说我们为了使得哈希表可以增容都会将除数设置为随着哈希表总长度而改变的变量，并且在不考虑其他因素的情况下，除数==容量的情况可以最大程度的利用空间。

平方取中法

  假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址； 再比如关键字为 4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合：不知 道关键字的分布，而位数又不是很大的情况。

折叠法

  折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加 求和，并按散列表表长，取后几位作为散列地址。 折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况。
  初次之外还有很多哈希方法，但是除了直接定址法和除留余数法外其他都不常用，所以可以仅作了解。

哈希冲突

  我们在利用哈希函数进行寻址的时候，很容易发生一种情况，就是两个数同时可能会寻到同一块地址，例如我们使用除留余数法进行寻址，除数为11，现在有key为11和22，余数都为0，我们都要存在地址为0的位置上，此时该怎么办呢，我们一个位置又不能存储两个数啊，于是这里就牵扯到了如何解决哈希冲突。哈希冲突的解决可以分为两大类，闭散列和开散列。

负载因子

  在具体讨论哈希冲突解决方法前我们还要关心一个概念即负载因子，一会我们就会知道无论是采用哪种哈希函数使用闭散列解决哈希冲突还是开散列解决哈希冲突，哈希表总会有被存满的时候，尤其是采用闭散列的时候，如果存放数据越多，就会发生越来越多的冲突，我们在解决起来可能就要遍历整张表，使得哈希表的性能下降，因此我们要尽可能避免一张哈希表被存满，不过这种情况虽然对于开散列来说可能还好，但是一段哈希表为了维持性能也一定是有它的负载上限的，这里就要对哈希表进行扩容，那么什么时候扩容怎么扩容就成了问题。我们先说如何解决什么时候扩容的难题。
  假设我们现在使用除留余数法在一段长为c的线性空间上进行散列，此时为了充分利用空间和使得可以增容，我们的除数不定，与容量保持一致也为c，于是此时的哈希函数为Hash(key) = key % c；我们所采用的冲突解决方法为线性探测法。为了避免大面积冲突降低性能，我们引入负载因子的概念，负载因子 = _size / c,(_size为哈希表中有效结点的个数)。这个公式可知负载因子是不可能大于1的，等于1时则哈希表已满，那么我们必须选取一个合适的值，当哈希表还没满，性能降低还不太明显的时候就进行增容，当然增容也不能太过频繁，因为哈希表的增容也会付出很大代价，一般来说对于闭散列我们的负载因子要求其大于等于0.8就可以开始增容了。
  说完什么时候增容，再说怎么增容。假如增容一次容量扩大一倍，可以知道的是，增容一次除数就会改变一次，那么原本算好地址的元素在新的哈希表中的地址也许就会改变，我们不得不遍历所有元素重新计算他们的地址然后再放到新的哈希表中，这也是为什么不能过于频繁的增容会有极大消耗的原因。

闭散列

  闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那 么可以把key存放到冲突位置中的“下一个” 空位置中去，于是问题就变成了如何找到一个合适的空位置让我们存储当前数据，还能保证我们在查找时能够再次准确的找到当前位置。

线性探测再散列

  线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。 例如除留余数法除数为11，key为11和22，当11先散列要存储在地址为0的位置时，22再进行散列的时候发现地址为0的位置已经存储过11的数据了，则它就继续向后线性探索，直到找到第一个空位置就将22的数据存储进去。

二次探测再散列

  线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位置的方式就 是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法为： Hi= (H0 + i ^ 2) % m, 或者：H0 = (Hi - i ^ 2) % m。其中： i = 1,2,3… ， H0是通过散列函数Hash(x)对元素的关键码key进行计算得到的位置，m是表的大小。

基于闭散列实现哈希表

  这里使用除留余数法+线性探测法实现哈希表。在实现时要注意为了标记散列表一个位置当前是否已经存在元素，我们要给每个结点都附加一个状态值，空/存在/删除三种状态，空和存在状态很好理解，删除状态的定义是为了方便再哈希表中删除结点所定义的状态，因为如果我们直接删除一个结点的话可能会影响其他结点的查找，因此我们一般删除都是采用该表状态为删除状态的这种伪删除法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
hash.hpp:
#pragma once
#include <iostream>
#include <vector>
#include <utility>

//定义三种状态，DELETE状态是为了方便我们对结点进行删除
enum STATE
{
    EMPTY,
    EXIST,
    DELETE
};

template<class K, class V>
struct HashNode
{
    //为了更好的可以找到映射，哈希表往往存的是一个K-V结构
    std::pair<K, V> _data;
    //状态默认为空
    STATE _state = EMPTY;
};

template<class K, class V>
class HashTable
{
public:
    typedef HashNode<K, V> Node;
    HashTable(const size_t n = 10)
        :_size(n)
    {
        _ht.resize(n);
    }
    bool Insert(const std::pair<K, V>& data)
    {
        //检查容量
        checkCapacity();
        //计算索引，进行散列
        int index = data.first % _ht.size();
        //1、判断当前地方是否有元素，没有直接插入
        //元素可以放在EMPTY和DELETE
        while(_ht[index]._state == EXIST)
        {
            //2、如果有，判断当前位置的元素的key是否和插入的相同，如果相同则插入失败直接返回
            if (_ht[index]._data.first == data.first)
            {
                //插入失败
                return false;
            }
            //3、如果有，且key不同则利用哈希冲突解决方法解决哈希冲突
            ++index;
            if(index == _ht.size())
            {
                index = 0;
            }
        }
        //元素插入
        _ht[index]._data = data;
        _ht[index]._state = EXIST;
        ++_size;
        return true;
    }
    //检查容量，负载因子超过阈值则扩容
    void checkCapacity()
    {
        //这里选取负载因子大于等于0.8扩容
        if(_ht.size() == 0 || _size * 10 / _ht.size() >= 8)
        {
            //增容
            int newC = _ht.size() == 0 ? 10 : 2 * _ht.size();
            HashTable<K, V> newHt(newC);
            //旧元素插入到新表
            for(int i = 0; i < _ht.size(); i++)
            {
                if(_ht[i]._state == EXIST)
                {
                    newHt.Insert(_ht[i]._data);
                }
            }
            //_ht = newHt._ht;深拷贝，太慢了，直接交换值比较快
            std::swap(_ht, newHt._ht);
        }
    }
    //搜索
    Node* Find(const K& key)
    {
        int index = key % _ht.size();
        while(_ht[index]._state != EMPTY)
        {
            if(_ht[index]._state == EXIST)
            {
                if(_ht[index]._data.first == key)
                {
                    return &_ht[index];
                }
            }
            index++;
            if(index == _ht.size())
            {
                index = 0;
            }
        }
        return nullptr;
    }
    //删除
    bool Erase(const K& key)
    {
        Node* pos = find(key);
        if(pos)
        {
            pos->_state = DELETE;
            --_size;
            return true;
        }
        return false;
    }
private:
    //散列表
    std::vector<Node> _ht;
    size_t _size;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
test.cpp:
#include "hash.hpp"
void test()
{
    HashTable<int, int> ht;
    ht.Insert(std::make_pair(5, 5));
    ht.Insert(std::make_pair(1, 1));
    ht.Insert(std::make_pair(0, 0));
    ht.Insert(std::make_pair(10, 10));
    ht.Insert(std::make_pair(30, 30));
    ht.Insert(std::make_pair(32, 32));
    ht.Insert(std::make_pair(8, 8));
    ht.Insert(std::make_pair(110, 110));
    ht.Insert(std::make_pair(23, 23));
    ht.Insert(std::make_pair(24, 23));
    ht.Insert(std::make_pair(25, 23));
    ht.Insert(std::make_pair(26, 23));
    HashNode<int, int>* node =  ht.Find(32);
    if(node != nullptr)
    {
        std::cout << (node->_data.first) << " " << node->_data.second;
    }
    else
    {
        std::cout << "nullptr" << std::endl;
    }
    std::cout << std::endl;
    node =  ht.Find(110);
    if(node != nullptr)
    {
        std::cout << (node->_data.first) << " " << node->_data.second;
    }
    else
    {
        std::cout << "nullptr" << std::endl;
    }
    
}
int main()
{
    test();
}


32 32
110 110

开散列

  开散列：也叫哈希桶或拉链法。开散列相比闭散列，可以更加有效的解决哈希冲突，因为其的结构是在哈希表的每一个节点上添加一个链表，所有经过哈希函数计算得出地址的结点直接添加到对应的链表上即可，这样一个地址上就不止可以存放一个元素，而是可以存放无限个，更好的处理了哈希冲突。其结构如下：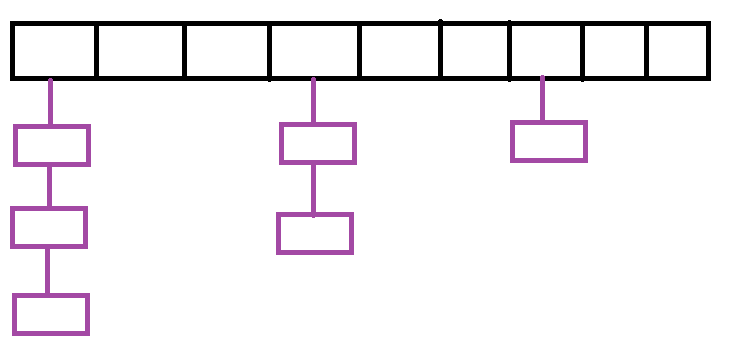

哈希桶

  要注意虽然哈希桶每个结点下面可以挂无数个结点，但是这里的单链表不易过长，否则每次查找结点都要遍历单链表，性能又会有很大程度的降低，于是我们还是需要利用负载因子进行扩容处理。
  对于开散列来说我们还是不得不遍历所有结点然后重新计算地址，但是有一种可以减少消耗的方法。本来我们需要遍历完原哈希表所有结点，然后依次释放原哈希表上每个链表的空间，再在新的哈希表上开辟新空间插入结点，但是这样一释放一申请的举动无异于脱裤子放屁，我们可以直接将原哈希表上的结点连接到新哈希表上，省去释放空间再申请空间的步骤，毕竟链表结点与结点之间本来就不一定是连续的，所以这样的操作替我们节省了很多开销。
  这里使用除留余数法实现哈希桶。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#pragma once
#include <iostream>
#include <utility>
#include <vector>
template<class K, class V>
//这里现在存的就是链表结点
//这里我们使用单链表就行了
struct HashNode
{
    HashNode(const std::pair<K, V>& data = std::pair<K, V>())
        :_data(data)
        ,_next(nullptr)
    {
    }
    std::pair<K, V> _data;
    HashNode<K, V>* _next;
};
template<class K, class V>
class HashTable
{
public:
    typedef HashNode<K, V> Node;
    HashTable(size_t n = 10)
        :_size(0)
    {
        _ht.resize(n);
    }
    //插入
    bool Insert(const std::pair<K, V>& data)
    {
        //检查负载因子，超过阈值进行扩容
        CheckCapacity();
        //计算位置
        int index = data.first % _ht.size();
        //遍历单链表
        Node* cur = _ht[index];
        while(cur)
        {
            if(cur->_data.first == data.first)
            {
                return false;
            }
            cur = cur->_next;
        }
        //插入，这里用头插其实比较方便，尾插也可以
        cur = new Node(data);
        cur->_next = _ht[index];
        _ht[index] = cur;
        ++_size;
        return true;
    }
    //查找
    Node* Find(const K& key)
    {
        int index = key % _ht.size();
        Node* cur = _ht[index];
        while(cur)
        {
            if(cur->_data.first == key)
            {
                return cur;
            }
            cur = cur->_next;
        }
        return nullptr;
    }
    //删除
    bool Erase(const K& key)
    {
        int index = key % _ht.size();
        Node* cur = _ht[index];
        Node* parent = nullptr;
        while(cur)
        {
            if(cur->_data.first == key)
            {
                //删除
                if(parent == nullptr)
                {
                    _ht[index] = cur->_next;
                }
                else
                {
                    parent->_next = cur->_next;
                }
                delete cur;
                --_size;
                return true;
            }
            parent = cur;
            cur = cur->_next;
        }
        return false;
    }
    void CheckCapacity()
    {
        //这里的阈值可以设置的稍微高一些，毕竟哈希桶的冲突不会像闭散列呢样严重
        //这里我们设定为插入元素数 >= 哈希表总长度时扩容
        if(_size >= _ht.size())
        {
            //扩容
            size_t newC = _ht.size() == 0 ? 10 : 2 * _ht.size();
            std::vector<Node*> newHt;
            newHt.resize(newC);
            //搬运数据，将原哈希表中的结点连接到新哈希表上
            for(int i = 0; i < _ht.size(); i++)
            {
                Node* cur = _ht[i];
                while(cur)
                {
                    int index = cur->_data.first % newHt.size();
                    Node* next = _ht[i]->_next;
                    //头插进新表
                    cur->_next = newHt[index];
                    newHt[index] = cur;
                    cur = next;
                }
                _ht[i] = nullptr;
            }
            //_ht = newHt;   //这里会进行深拷贝，消耗很大，为了防止深拷贝我们直接交换
            std::swap(_ht, newHt);
        }
    }

private:
    //此时哈希表就相当于一个链表指针数组
    std::vector<Node*> _ht;
    size_t _size;
};

封装

  最后我们再将我们写好的哈希桶封装为unordered_map/unordered_set。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
hash_bucketMod.hpp:
#pragma once
#include <iostream>
#include <utility>
#include <vector>
//这里现在存的就是链表结点
//这里我们使用单链表就行了
//这里依然为了更好的封装对原有的哈希桶进行了修改
template<class V>
struct HashNode
{
    HashNode(const V& data = V())
        :_data(data)
        ,_next(nullptr)
    {
    }
    V _data;
    HashNode<V>* _next;
};
template<class K, class V, class KeyOfCalue>
class HashTable;
template<class K, class V, class KeyOfValue>
class _HashIterator
{
public:
    typedef HashNode<V> Node;
    typedef _HashIterator<K, V, KeyOfValue> Self;
    typedef HashTable<K, V, KeyOfValue> HTable;
    _HashIterator(Node* node, HTable* pht)
        :_node(node)
        ,_pht(pht)
    {
    }
    V& operator*()
    {
        return _node->_data;
    }
    V* operator->()
    {
        return &_node->_data;
    }
    bool operator!=(const Self& it)
    {
        return _node != it._node;
    }
    Self& operator++()
    {
        if(_node->_next)
        {
            _node = _node->_next;
        }
        else
        {
            KeyOfValue kov;
            //找到下一个非空链表头
            //1、首先确定当前迭代器在哈希表中的位置
            int index = kov(_node->_data) % _pht->_ht.size();
            ++index;
            while(index < _pht->_ht.size())
            {
                if(_pht->_ht[index])
                {
                    _node = _pht->_ht[index];
                    break;
                }
                ++index;
            }
            if(index == _pht->_ht.size())
            {
                _node = nullptr;
            }
        }
        return *this;
    }
private:
    Node* _node;
    HTable* _pht;
};
template<class K, class V, class KeyOfValue>
class HashTable
{
    friend class _HashIterator<K, V, KeyOfValue>;
public:
    typedef HashNode<V> Node;
    typedef _HashIterator<K, V, KeyOfValue> iterator;
    //迭代器相关
    iterator begin()
    {
        for(int i = 0; i < _ht.size(); i++)
        {
            if(_ht[i] != nullptr)
            {
                return iterator(_ht[i], this);
            }
        }
        return iterator(nullptr, this);
    }
    iterator end()
    {
        return iterator(nullptr, this);
    }
    HashTable(size_t n = 10)
        :_size(0)
    {
        _ht.resize(n, nullptr);
    }
    //插入
    std::pair<iterator, bool> Insert(const V& data)
    {
        //检查负载因子，超过阈值进行扩容
        CheckCapacity();
        //计算位置
        KeyOfValue kov;
        int index = kov(data) % _ht.size();
        //遍历单链表
        Node* cur = _ht[index];
        while(cur)
        {
            if(kov(cur->_data) == kov(data))
            {
                return std::make_pair(iterator(cur, this), false);
            }
            cur = cur->_next;
        }
        //插入，这里用头插其实比较方便，尾插也可以
        cur = new Node(data);
        cur->_next = _ht[index];
        _ht[index] = cur;
        ++_size;
        return std::make_pair(iterator(cur, this), true);
    }
    //查找
    Node* Find(const K& key)
    {
        KeyOfValue kov;
        int index = key % _ht.size();
        Node* cur = _ht[index];
        while(cur)
        {
            if(kov(cur->_data) == key)
            {
                return cur;
            }
            cur = cur->_next;
        }
        return nullptr;
    }
    //删除
    bool Erase(const K& key)
    {
        int index = key % _ht.size();
        Node* cur = _ht[index];
        Node* parent = nullptr;
        KeyOfValue kov;
        while(cur)
        {
            if(kov(cur->_data) == key)
            {
                //删除
                if(parent == nullptr)
                {
                    _ht[index] = cur->_next;
                }
                else
                {
                    parent->_next = cur->_next;
                }
                delete cur;
                --_size;
                return true;
            }
            parent = cur;
            cur = cur->_next;
        }
        return false;
    }
    void CheckCapacity()
    {
        //这里的阈值可以设置的稍微高一些，毕竟哈希桶的冲突不会像闭散列呢样严重
        //这里我们设定为插入元素数 >= 哈希表总长度时扩容
        if(_size >= _ht.size())
        {
            //扩容
            size_t newC = _ht.size() == 0 ? 10 : 2 * _ht.size();
            std::vector<Node*> newHt;
            newHt.resize(newC);
            KeyOfValue kov;
            //搬运数据，将原哈希表中的结点连接到新哈希表上
            for(int i = 0; i < _ht.size(); i++)
            {
                Node* cur = _ht[i];
                while(cur)
                {
                    int index = kov(cur->_data) % newHt.size();
                    Node* next = _ht[i]->_next;
                    //头插进新表
                    cur->_next = newHt[index];
                    newHt[index] = cur;
                    cur = next;
                }
                _ht[i] = nullptr;
            }
            //_ht = newHt;   //这里会进行深拷贝，消耗很大，为了防止深拷贝我们直接交换
            std::swap(_ht, newHt);
        }
    }

private:
    //此时哈希表就相当于一个链表指针数组
    std::vector<Node*> _ht;
    size_t _size;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
unordered_map.hpp:
#pragma once
#include "hash_bucketMod.hpp"
template<class K, class V>
class Unordered_Map
{
    struct MapKeyOfValue
    {
        const K& operator()(const std::pair<K, V>& data)
        {
            return data.first;
        }
    };
public:
    typedef typename HashTable<K, std::pair<K, V>, MapKeyOfValue>::iterator iterator;
    iterator begin()
    {
        return _ht.begin();
    }
    iterator end()
    {
        return _ht.end();
    }
    std::pair<iterator, bool> Insert(const std::pair<K, V>& data)
    {
        return _ht.Insert(data);
    }
    V& operator[](const K& key)
    {
        return (_ht.Insert(std::make_pair(key, V())).first)->second;
    }
private:
    HashTable<K, std::pair<K, V>, MapKeyOfValue> _ht;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
unordered_set.hpp:
#pragma once
#include "hash_bucketMod.hpp"
template<class K>
class Unordered_set
{
    struct SetKeyOfValue
    {
        const K& operator()(const K& data)
        {
            return data;
        }
    };
public:
    typedef typename HashTable<K, K, SetKeyOfValue>::iterator iterator;
    iterator begin()
    {
        return _ht.begin();
    }
    iterator end()
    {
        return _ht.end();
    }
    std::pair<iterator, bool> Insert(const K& data)
    {
        return _ht.Insert(data);
    }
private:
    HashTable<K, K, SetKeyOfValue> _ht;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
test.cpp:
#include "unordered_map.hpp"
#include "unordered_set.hpp"
void test3()
{
    Unordered_Map<int, int> umap;
    umap.Insert(std::make_pair(1, 1));
    umap.Insert(std::make_pair(5, 5));
    umap.Insert(std::make_pair(6, 6));
    umap.Insert(std::make_pair(9, 9));
    for(auto e : umap)
    {
        std::cout << e.first << " " << e.second << std::endl;
    }
    umap[6] = 11;
    umap[10] = 10;
    umap[25] = 1;
    std::cout << std::endl;
    for (auto e : umap)
    {
        std::cout << e.first << " " << e.second << std::endl;
    }
    Unordered_set<int> uset;
    uset.Insert(1);
    uset.Insert(5);
    uset.Insert(6);
    uset.Insert(9);
    std::cout << std::endl;
    for (auto e : uset)
    {
        std::cout << e << std::endl;
    }
}
int main()
{
    test3();
}


1 1
5 5
6 6
9 9

10 10
1 1
25 1
5 5
6 11
9 9

1
5
6
9

  从结果上来看我们的实现目前成功了。

总结

  通过这两章对关联式容器两种底层原理的探索和实现我们可以总结出以下结论。
  1、普通版本的map/set底层使用的红黑树可以将搜索、插入和删除的操作时间复杂度优化为OlogN。
  2、要求map/set中的key必须是可以比较的，不然就无法达成二叉搜索树中需要比较大小的操作，那么就无法成立红黑树。
  3、unordered系列的map/set底层结构是一个哈希桶，可以将搜索、插入和删除的操作优化为O1，但是在每次需要增容的时候则不得不需要执行一次On的遍历操作，代价极大。
  4、unordered系列的map/set插入数据的key要求必须有合适的哈希函数能够对其进行哈希，否则将无法计算出合适的下标存储数据，例如我们实现的时候写死了哈希函数，因此其只能存储key可以取模的数据，而如果key是一个字符串我们将束手无策，不过也有字符串的哈希方法，会将字符串转为整数在进行哈希，这里不再深入讨论。
  5、map/set可以对数据根据key进行排序，且每次操作的事件复杂度十分平均都为OlogN；unordered_map/unordered_set不会对数据进行排序，虽然大多数情况下的操作都是O1的，但是一旦在插入时遇到增容的情况，则会造成极大消耗从而变成ON的时间复杂度，同时unordered系列有可能会消耗更多的内存空间。

-------------本文结束感谢您的阅读!-------------
记录学习每一分，感谢您的赞助