第二章 顺序表和链表
顺序表
什么是顺序表
顺序表是物理地址全部连续的存储数据的方式。顺序表分为动态顺序表以及动态的顺序表,静态的顺序表一般很少使用,因为其大小一旦固定不能再进行改变。
顺序表在开发中十分经常使用,因为其方便简单,并且易于操作。数组就是顺序表的一种,因为其在逻辑结构上是线性的,在物理结构上是连续的。由于十分常用在Cpp的STL库中封装了以顺序表为数据结构的vector容器供我们使用。
实现
顺序表的实现十分类似于vector类的实现。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209#include <iostream>
#include <stdlib.h>
#include <assert.h>
#include <stdlib.h>
#include <Windows.h>
using namespace std;
#define N 100
//顺序表的实现
//十分类似于我们实现过的vector类,毕竟vector就是顺序表
template<class T>
class SeqList
{
public:
//构造函数
SeqList()
:_array(nullptr)
,_size(0)
,_capacity(0)
{}
//析构函数
~SeqList()
{
if(_array != nullptr)
{
delete _array;
}
}
//pos前插入
void Insert(size_t pos, const T& value)
{
//判断pos是否合法
if(pos > _size || pos < 0)
{
return;
}
//扩容
Expend();
for(size_t i = _size; i > pos; i--)
{
_array[i] = _array[i - 1];
}
_array[pos] = value;
_size++;
}
//尾插
void Push_back(const T& value)
{
//扩容
Expend();
_array[_size] = value;
_size++;
}
//头插
void Push_front(const T& value)
{
//扩容
Expend();
//所有元素向后挪一个位置
for(size_t i = _size; i > 0; i--)
{
_array[i] = _array[i - 1];
}
_array[0] = value;
_size++;
}
//尾删
void Pop_back()
{
//删除前要先判断,有元素才能删
if(_size > 0)
{
_size--;
}
}
//头删
void Pop_front()
{
//有元素才能删
if(_size > 0)
{
for (size_t i = 1; i < _size; i++)
{
_array[i - 1] = _array[i];
}
_size--;
}
}
//删除pos当前位置数据
void Erase(size_t pos)
{
//pos不合法
if(pos >= _size || pos < 0)
{
return;
}
for(size_t i = pos; i < _size - 1; i++)
{
_array[pos] = _array[pos + 1];
}
_size--;
}
//查找
size_t Find(const T& value)
{
for(size_t i = 0; i < _size; i++)
{
if(_array[i] == value)
{
return i;
}
}
return -1;
}
//二分查找
size_t BinaryFind(const T& value)
{
//左闭右开区间
size_t high = _size, low = 0;
while(high > low)
{
size_t mid = (high + low) / 2;
if(_array[mid] == value)
{
return mid;
}
else if(_array[mid] > value)
{
high = mid;
}
else
{
low = mid + 1;
}
}
}
//修改
void Modify(size_t pos, const T& value)
{
if(pos < 0 || pos >= _size)
{
return;
}
_array[pos] = value;
}
//打印
void Print()
{
for(size_t i = 0; i < _size; i++)
{
cout << _array[i] << " ";
}
cout << endl;
//cout << _size << endl;
}
//当前元素个数
size_t Size()
{
return _size;
}
//某个位置的值
T& operator[](size_t pos)
{
assert(pos >=0 && pos < _size);
return _array[pos];
}
//冒泡排序
void BubbleSort()
{
for(int i = 0; i < _size - 1; i++)
{
bool flag = false;
for(int j = 0; j < _size - i - 1; j++)
{
if(_array[j] > _array[j + 1])
{
swap(_array[j], _array[j + 1]);
flag = true;
}
}
if(flag == false)
{
break;
}
}
}
void RemoveAll()
{
_size = 0;
}
private:
//T _array[N];//静态顺序表,利用数组,不可变,十分不灵活
T* _array;//动态顺序表,利用指针动态开辟
size_t _size;//长度
size_t _capacity;//容量
//扩容
void Expend()
{
if(_size == _capacity)//满了
{
size_t newCapacity = (_capacity == 0 ? 5 : 2 * _capacity);
//创建更大空间,拷贝,释放原有空间
_array = (T*)realloc(_array, newCapacity * sizeof(T));
//申请失败
assert(_array);
//更新容量
_capacity = newCapacity;
}
}
};
顺序表的优缺点
顺序表优点:
1、根据下标随机访问时间复杂度O(1)。
2、不会产生内存碎片。
3、代码简单。
4、在尾插时事件复杂度为O1。
顺序表缺点:
1、在中间插入时时间复杂度为On,最坏情况下要移动整个顺序表完成头插。
2、增容申请新空间进行数据拷贝再释放旧空间,有这不小消耗。
3、增容一次空间为原有空间两倍,可能会造成空间大量浪费。
链表
什么是链表
顺序表是物理地址连续的数据存储方式,而链表与之相反,链表存储数据的物理地址不一定连续,因此它不能像顺序表那样通过直接寻址的方式访问到数据,它通过指针来连接和组织数据,因此也使得它和顺序表有着截然不同的特征,并且相比顺序表来说或许更难理解一些。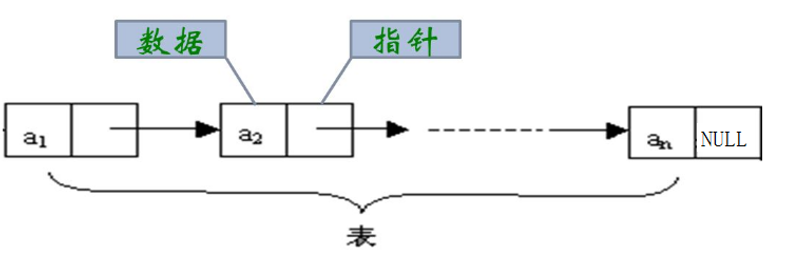
链表有着以下几种种类:
1、带头链表,不带头链表。
2、单向链表,双向链表。
3、循环链表,不循环链表。
他们组合搭配起来一共有8种组合,
由于链表的特性它可以很好地结局一些顺序表的缺点,比如他不需要扩容,并且更方便插入等等,但是在一些方面上它也有着不如顺序表的地方,关于优缺点我们放在最后再进行分析,接下来实现一个简单的带头单向不循环链表。
实现
在Cpp的STL中有一个list容器,其中实现了一个带头双向循环链表,这里我们简化进行实现带头单向不循环链表,思路更加简单(带头双向循环链表在Cpp章节中在模拟实现list时也有实现)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129#include <iostream>
using std::cout;
using std::endl;
template<class T>
struct ListNode
{
//构造函数
ListNode(const T& value = T())
:data(value)
,next(nullptr)
{
}
T data;//数据域
ListNode* next;//指针域,指向下一个节点
};
template<class T>
class List
{
public:
//构造函数
List()
:_head(new ListNode<T>)
,_size(0)
{
}
~List()
{
//依次删除所有节点以释放所有空间
while(_size > 0)
{
Pop_Front();
}
delete _head;
}
//头插
void Push_Front(const T& value)
{
InsertPos(0, value);
}
//尾插
void Push_Back(const T& value)
{
InsertPos(_size, value);
}
//打印所有数据
void PrintAll()
{
ListNode<T>* temp = _head->next;
while(temp != nullptr)
{
cout << temp->data << " ";
temp = temp->next;
}
cout << endl;
}
//在下标为pos的元素前进行插入
void InsertPos(size_t pos, const T& value)
{
if(pos < 0 || pos > _size)
{
cout << "InsertPos: pos error" << endl;
return;
}
//这里的插入时间复杂度本应是O1,但是由于链表不便于寻址因此又需要线性的时间进行寻址
ListNode<T>* node = FindForPos(pos);
if(node == nullptr)
{
return;
}
ListNode<T>* newNode = new ListNode<T>(value);
newNode->next = node->next;
node->next = newNode;
_size++;
}
//删除下标为pos的元素
void ErasePos(size_t pos)
{
if(pos < 0 || pos >= _size)
{
cout << "ErasePos: pos error" << endl;
return;
}
ListNode<T>* node = FindForPos(pos);
if(node == nullptr)
{
return;
}
ListNode<T>* temp = node->next;
node->next = temp->next;
delete temp;
_size--;
}
//尾删
void Pop_Back()
{
ErasePos(_size - 1);
}
//头删
void Pop_Front()
{
ErasePos(0);
}
//返回链表长度
size_t Size()
{
return _size;
}
private:
//返回下标为pos的元素的前一个元素,下标为0的元素则返回头节点
ListNode<T>* FindForPos(size_t pos)
{
ListNode<T> *temp = _head;
for(int i = 0; i < pos; i++)
{
//不存在,长度不够
if(temp == nullptr)
{
cout << "FindForPos: pos error" << endl;
return nullptr;
}
temp = temp->next;
}
return temp;
}
private:
ListNode<T>* _head;
size_t _size;
};
链表的优缺点
链表的优点:
1、链表在任意位置插入和删除时时间复杂度都能达到O1。
2、插入一个节点开辟一个空间,不牵扯扩容问题。
链表的缺点:
1、以节点为单位存储数据,并且还要存储指针可能会浪费更多空间。
2、不支持随机访问,因此在某一位置插入尽管插入只需要O1但是找到这个位置需要On。
3、思路实现略复杂。
链表反转问题
给一个单链表,反转这个单链表。
https://leetcode-cn.com/problems/reverse-linked-list/description/
反转链表有很多种方式,我们可以尾删所有结点并同时将他们重新头插回链表,但这样的思路消耗实在太高,我们每次尾插都不得不遍历整张单链表去找到尾,因此对其简化,这里提供两种思路,
第一种,后插头删法。这种方法是通过从第二个节点开始遍历整个链表,依次将节点移向头部的方法。图解如下: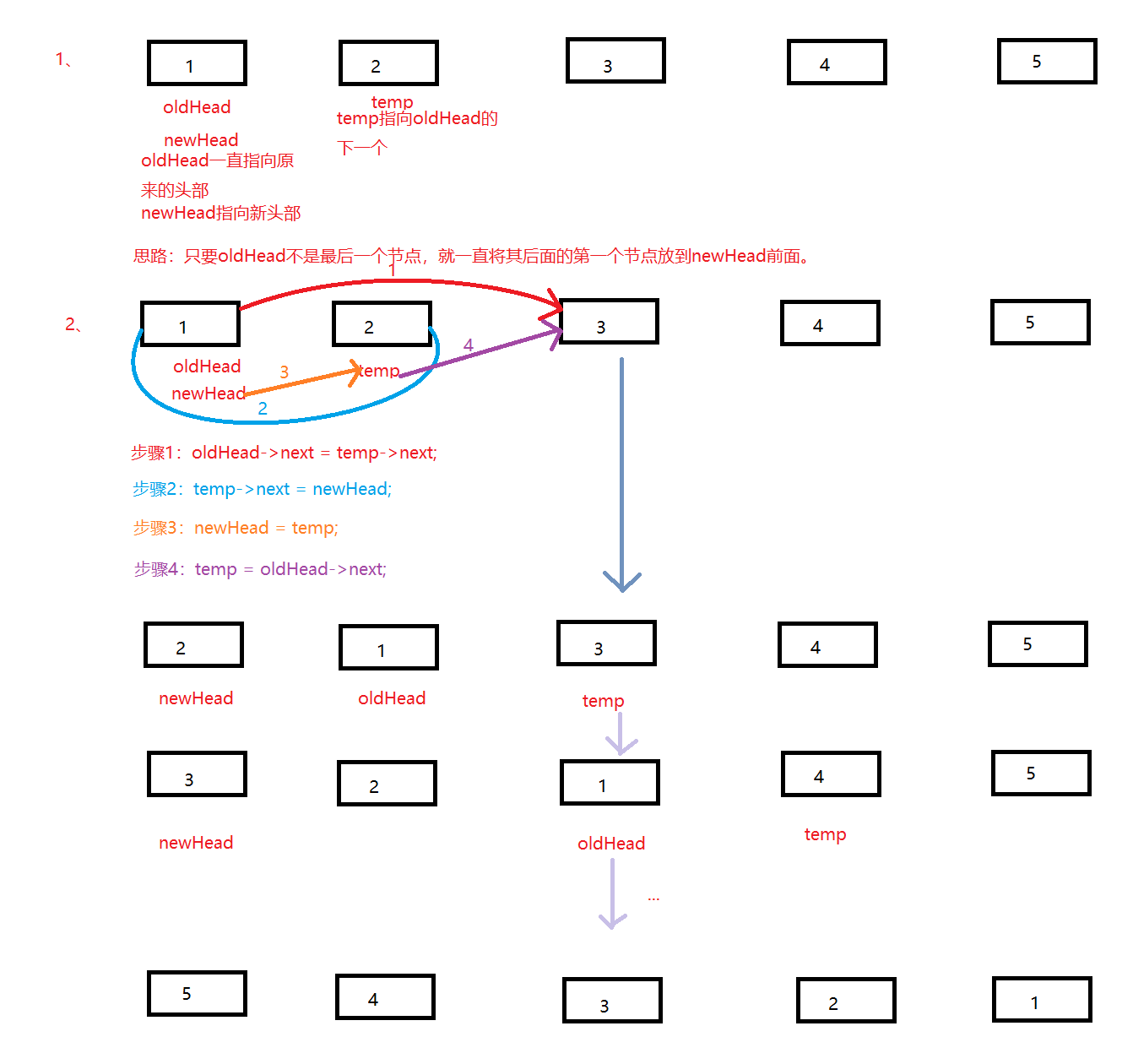
题解:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL)
{
return head;
}
ListNode* oldHead = head;
ListNode* temp = oldHead->next;
while(oldHead->next != NULL)
{
oldHead->next = temp->next;
temp->next = head;
head = temp;
temp = oldHead->next;
}
return head;
}
};
2、第二种:向后转法。第二种思路更为直观,我们就直接将每个结点中的next的指向改变即可。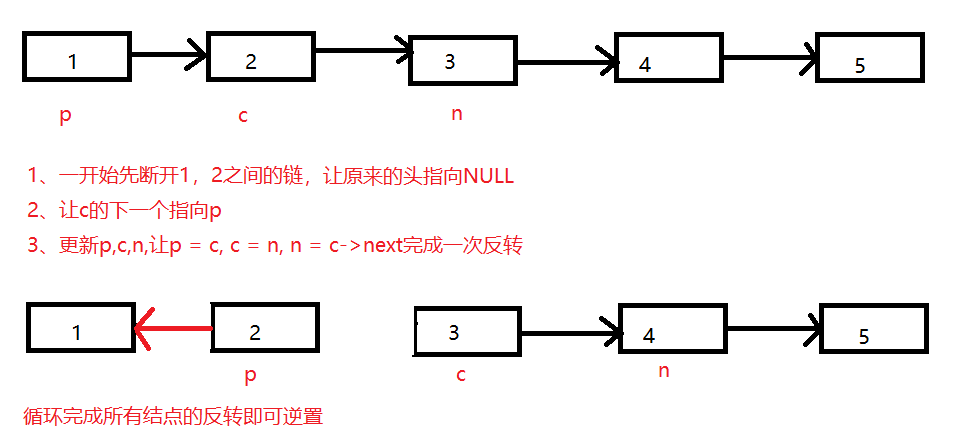
题解:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL)
{
return head;
}
ListNode* prev = head;
ListNode* cur = head->next;
ListNode* next = cur;
head->next = NULL;
while(cur != NULL)
{
next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
return prev;
}
};
链表有多种多样的问题,我会另开章节逐个归纳,就不再此继续罗列了。

